

Next: Infinite Body, 1-D, Steady-Periodic
Up: Library of Green's Functions
Previous: Plate, steady 1-D Helmholtz.
Helmholtz Equation: Steady-Periodic
In this section, steady-periodic heat conduction is treated. Also called
time-harmonic or thermal-wave behavior, this special case is important
whenever the causal effect is harmonic in time and has continued long
enough for any start-up transients to die out.
Rectangular Coordinates. Steady-periodic 1-D.
Consider a one-dimensional region in which the temperature is sought.
The transient temperature distribution satisfies
Here 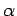 is the thermal diffusivity (m
is the thermal diffusivity (m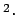 s
s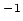 ),
),
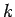 is the thermal conductivity (W
is the thermal conductivity (W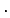 m
m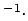 K
K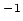 ),
),
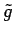 is the volume heating (W
is the volume heating (W m
m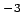 ),
and
),
and 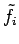 is a specified boundary condition.
Index
is a specified boundary condition.
Index 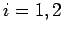 represents the boundaries at the limiting values
of coordinate
represents the boundaries at the limiting values
of coordinate 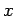 . The boundary condition may be one of three types
at each boundary: boundary type 1 is specified temperature
(
. The boundary condition may be one of three types
at each boundary: boundary type 1 is specified temperature
(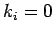 and
and 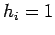 ); boundary type 2 is specified heat
flux (
); boundary type 2 is specified heat
flux (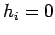 ); and, boundary type 3 is specified convection where
); and, boundary type 3 is specified convection where 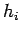 is a
constant-with-time heat transfer coefficient (or contact conductance).
is a
constant-with-time heat transfer coefficient (or contact conductance).
Since in this section the applications of interest involve steady-periodic
heating, the solution is sought in Fourier-transform space,
and the solution is interpreted as the steady-periodic response at
a single frequency 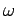 .
For further discussion of this point see Mandelis (2001, page 2-3).
Consider the Fourier transform of the above temperature equations:
.
For further discussion of this point see Mandelis (2001, page 2-3).
Consider the Fourier transform of the above temperature equations:
Here 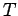 is the steady-periodic temperature,
is the steady-periodic temperature,
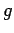 is the steady-periodic volume heating,
is the steady-periodic volume heating,
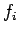 is the steady-periodic specified
boundary condition, and
is the steady-periodic specified
boundary condition, and 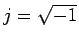 .
.
The temperature will be found with the Fourier-space
Green's function, defined by the following equations:
Here
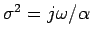 and
and 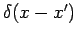 is the Dirac delta
function. The coefficient
is the Dirac delta
function. The coefficient 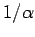 preceding the delta function in Eq. (3) provides the
1-D frequency-domain Green's function with units of s
preceding the delta function in Eq. (3) provides the
1-D frequency-domain Green's function with units of s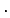 m
m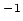 .
This is consistent with earlier work with time-domain Green's functions.
.
This is consistent with earlier work with time-domain Green's functions.
If the steady-periodic Green's function  is known (given below), then the
steady-periodic temperature is given by the following integral
equation:
is known (given below), then the
steady-periodic temperature is given by the following integral
equation:
For a derivation of this equation see Beck et al. (1992, pp. 40-43). Next
the steady-periodic Green's functions are given for 1-D bodies for cases XIJ.


Next: Infinite Body, 1-D, Steady-Periodic
Up: Library of Green's Functions
Previous: Plate, steady 1-D Helmholtz.
2004-08-10
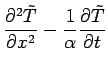
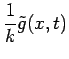
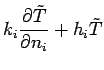
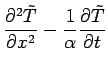
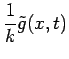
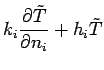
![]() .
For further discussion of this point see Mandelis (2001, page 2-3).
Consider the Fourier transform of the above temperature equations:
.
For further discussion of this point see Mandelis (2001, page 2-3).
Consider the Fourier transform of the above temperature equations:
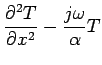
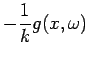
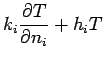
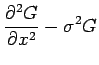
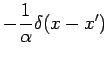
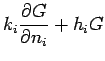
![]() is known (given below), then the
steady-periodic temperature is given by the following integral
equation:
is known (given below), then the
steady-periodic temperature is given by the following integral
equation:
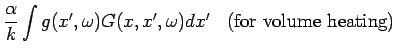
![$\displaystyle + \alpha f_i(\omega) \times
\left[
\begin{array}{ll}
\partial G /...
...}{k} G(x, x_i, \omega)
& \mbox{(type 2 or 3)}
\end{array}\right] \;\;\; i = 1,2$](img40.png)