GX11(x ![$\displaystyle \begin{array}{cc}\sinh [m(L-x^{\prime })]\sinh mx/(m\sinh mL) & ...
...h [m(L-x)]\sinh mx^{\prime }/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}$](img632.gif)
|
GX11(x ![$\displaystyle \begin{array}{cc}\sinh [m(L-x^{\prime })]\sinh mx/(m\sinh mL) & ...
...h [m(L-x)]\sinh mx^{\prime }/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}$](img632.gif)
|
GX12(x ![$\displaystyle \begin{array}{cc}\cosh [m(L-x^{\prime })]\sinh mx/(m\cosh mL) & ...
...h [m(L-x)]\sinh mx^{\prime }/(m\cosh mL) & \text{for }x>x^{\prime }\end{array}$](img635.gif)
|
GX13(x ![$\displaystyle \begin{array}{c}\frac{1}{m}[\cosh m(L-x^{\prime })+\frac{B_{2}}{...
...\cosh mL+\frac{B_{2}}{mL}\sinh mL]\text{; \space for }x>x^{\prime }\end{array}$](img638.gif)
|
GX21(x ![$\displaystyle \begin{array}{cc}\cosh (mx)\sinh [m(L-x^{\prime })]/(m\cosh mL) ...
...})\sinh [m(L-x^{\prime })]/(m\cosh mL) & \text{for }x>x^{\prime }\end{array}$](img641.gif)
|
X22 Plate,
![]() G/
G/![]() x = 0 (Neumann) at both
sides.
x = 0 (Neumann) at both
sides.
GX22(x ![$\displaystyle \begin{array}{cc}\cosh (mx)\cosh [m(L-x^{\prime })]/(m\sinh mL) ...
...(mx^{\prime })\cosh [m(L-x)]/(m\sinh mL) & \text{for }x>x^{\prime }\end{array}$](img644.gif)
|
GX23(x 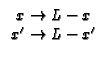
|
| For x < x |
|||
![$\displaystyle {\frac{(mL+B_{2})\left[ e^{m(x^{\prime }-x+2L)}+e^{m(2L-x-x^{\pri...
...mL-B_{2})2e^{m(x^{\prime }-x)}}{2m\left[
(mL+B_{2})e^{2mL}-(mL-B_{2})\right] }}$](img649.gif) |
|||
| For x < x |
|||
![$\displaystyle {\frac{(mL+B_{2})\left[ e^{m(x-x^{\prime }+2L)}+e^{m(2L-x-x^{\pri...
...mL-B_{2})2e^{m(x-x^{\prime })}}{2m\left[
(mL+B_{2})e^{2mL}-(mL-B_{2})\right] }}$](img650.gif) |
X31 Plate,
- k![]() G/
G/![]() x + h1G = 0
(convection) at x = 0 and
x + h1G = 0
(convection) at x = 0 and
![]() G/
G/![]() x = 0 (Neumann) at x = L. Note
B1 = h1L/k.
x = 0 (Neumann) at x = L. Note
B1 = h1L/k.
| For x < x |
|||
![$\displaystyle {\frac{(mL+B_{1})\left[ e^{m(x-x^{\prime }+2L)}-e^{m(x+x^{\prime ...
...}-e^{m(x-x^{\prime })}\right] }{2m%
\left[ (mL+B_{1})e^{2mL}+mL-B_{1}\right] }}$](img651.gif) |
|||
| For x < x |
|||
![$\displaystyle {\frac{(mL+B_{1})\left[ e^{m(x^{\prime }-x+2L)}-e^{m(x+x^{\prime ...
...}-e^{m(x^{\prime }-x)}\right] }{2m%
\left[ (mL+B_{1})e^{2mL}+mL-B_{1}\right] }}$](img652.gif) |
| For x < x |
|||
![$\displaystyle {\frac{(mL+B_{1})\left[ e^{m(x-x^{\prime }+2L)}+e^{m(x+x^{\prime ...
...e^{m(x-x^{\prime })}\right] }{2m%
\left[ (mL+B_{1})e^{2mL}-(mL-B_{1})\right] }}$](img653.gif) |
|||
| For x < x |
|||
![$\displaystyle {\frac{(mL+B_{1})\left[ e^{m(x^{\prime }-x+2L)}+e^{m(x+x^{\prime ...
...e^{m(x^{\prime }-x)}\right] }{2m%
\left[ (mL+B_{1})e^{2mL}-(mL-B_{1})\right] }}$](img654.gif) |
| For x | < | x |
|
| x |
|||
| + (m2L2 + B1mL + B2mL + B1B2)em(x - x |
|||
| + (m2L2 + B1mL - B2mL + B1B2)e-m(x - x |
|||
| ÷ |
|||
| For x | > | x |
|
| x |
|||
| + (m2L2 + B1mL + B2mL + B1B2)em(x |
|||
| + (m2L2 + B1mL - B2mL + B1B2)e-m(x |
|||
| ÷ |