

Next: Representations of .
Up: Dirac delta function
Previous: Dirac delta function
- Sifting property. Given function
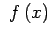 continuous at
continuous at
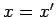 ,
,
When integrated, the product of any (well-behaved) function and the Dirac
delta yields the function evaluated where the Dirac delta is singular. The
sifting property also applies if the arguments are exchanged:
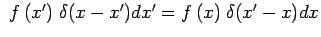 .
.
- Integral.
where 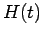 is the Heaviside unit step function defined as
is the Heaviside unit step function defined as
- Units. Since the definition of the Dirac delta requires that the
product
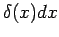 is dimensionless, the units of the Dirac delta are
the inverse of those of the argument
is dimensionless, the units of the Dirac delta are
the inverse of those of the argument 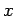 . That is,
. That is, 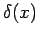 has units
has units 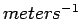 , and
, and 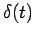 has units
has units 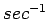 .
.
- Definition for radial, 2-D, and 3-D geometries. For two- and three-
dimensional problems with vector coordinate
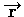 ,
the Dirac delta function is defined:
,
the Dirac delta function is defined:
where 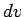 is differential volume. The units of
is differential volume. The units of
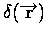 are given by [
are given by [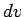 ]
]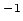 , and three important cases are the
listed below.
, and three important cases are the
listed below.
- 1-D radial cylindrical coordinates:
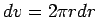 , and units of
, and units of
 are [meters]
are [meters] .
.
- 1-D radial spherical coordinates:
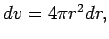 and units of
and units of
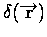 are [meters]
are [meters]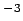 .
.
- 2-D Cartesian coordinates:
dv = dx dy,
and units of
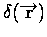 are [meters]
are [meters]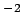 .
.


Next: Representations of .
Up: Dirac delta function
Previous: Dirac delta function
2004-01-21
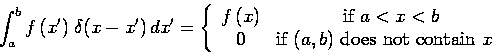
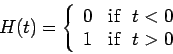
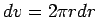 , and units of
, and units of
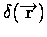 are [meters]
are [meters]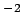 .
.
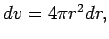 and units of
and units of
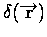 are [meters]
are [meters]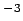 .
.
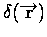 are [meters]
are [meters]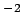 .
.